RELAX NG Implementation Cook Book: Day 3

From the higher view point, the validation algorithm works in the following way: the input for this algorithm is a sequence of elements, attributes and text chunks in the document order.

The algorithm keeps an Expression as its internal state. It also has a stack to keep Expressions. ^[1] It reads the input sequence one by one, and updates its internal state accordingly. Thus this algorithm works nicely with both SAX and DOM.

If a document is invalid, then the algorithm rapidly detects it (fail-fast). Thus you can know that the document is invalid at the earilest possible timing. When the entire document is processed without an error, then it means the document was valid.

The following figure illustrates this.

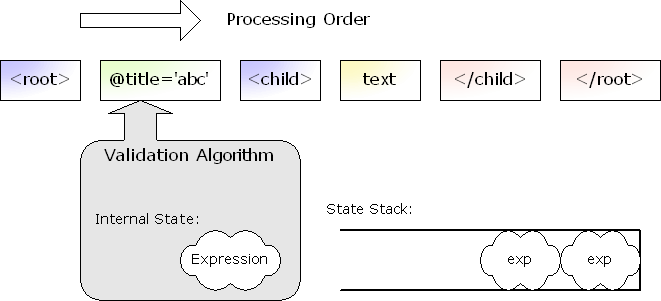Today, we'll examine various concepts that are necessary to implement a validator, and then implement a simple validator. Tomorrow, we'll discuss the ambiguous grammar and extend the validator to a fully-fledged one that can deal with such a situation.

The first concept we define is the nullability. An Expression is said to be nullable if it can match the empty input sequence. For example, (a,b)?,c* is nullable and (a|(b,c)*) is nullable, but a+ is not (assuming that a,b, and c are ElementExps.)

Nullability can be easily implemented recursively. <empty> and <text> are by definition nullable. All other non-combinators (element,attribute,data,value and notAllowed) are not nullable. ^[2]

Nullability of combinators is mostly intuitive. For example, guess when (A|B) is nullable? It is nullable if A or B is nullable. (A,B) and A&B are nullable only when both A and B are nullable. (A+) is nullable if A is nullable.

ListExp is the only difficult one. In short, we define that ListExp is always non-nullable nogardless of its children. I know it sounds strange, but actually this is correct [why?].

Well, then let's implement a method that checks nullability of the expression. In Java, for example, you can add an abstract isNullable method to the Expression class and implement it in all derived classes.

The second concept, which is by far the most important, is a derivative of an expression. Some people calls this concept as residual.

Let me try an informal explanation first: consider an expression foo,(bar|zot) and an input sequence. If the first token in the input sequence is foo, then the rest of the sequence should match (bar|zot). Now, this is what we call "derivative"; we say "(bar|zot) is a derivative of foo,(bar|zot) by foo".

Let's have a little quiz to test your understanding:

This derivative computation applies to element tokens and character chunk tokens.

You might think that it must be hard to compute derivatives, but actually, it can be computed recursively. From now on, I'll use d(X) to denote a derivative of X by the current input token.

I'll explain the precise definition later. For now, all you need is a grip on what we're trying to do.

Since RELAX NG treats attributes and elements uniformly, one can think of derivatives by attributes. But since attributes are orderless, the derivative computation for attributes slightly differs from that for elements.

For example, the derivative of foo,bar by bar is ##notAllowed while the derivative of @foo,@bar by @bar is @foo.

The precise algorithm will be given later.

Given a content model, "head elements" are those elements which can appear first. For example, consider a content model: foo?,(bar|zot+),tty. Since {foo,bar,tty} is a valid sequence for this content model, foo is a head element. From the similar reasoning, bar and zot are also head elements. Since no valid sequence can start with tty, it is not a head element.

Computation of head elements can be implemented easily by using recursion. In other words, this computation can be thought as a function that takes a pattern as a parameter and returns a set of ElementExps.

For example,

h(foo?,(bar|zot+),tty)

= h(foo?,(bar|zot+)) because foo?,(bar|zot)+ is not nullable.

= h(foo?) ∪ h(bar|zot+) because foo? is nullable.

= h(foo?) ∪ h(bar) ∪ h(zot+)

= h(foo?) ∪ h(bar) ∪ h(zot)

= h(foo?) ∪ h(bar) ∪ {zot}

= h(foo?) ∪ {bar} ∪ {zot}

= h(foo?) ∪ {bar,zot}

= h(foo) ∪ h(##empty) ∪ {bar,zot} because foo? is internally represented as foo|##empty)

= {foo} ∪ {} ∪ {bar,zot}

= {foo,bar,zot}

class HeadElementsCalc : ExpVisitor {
  Set headElements;
  
  void onChoice( ChoiceExp exp ) {
    exp.exp1.visit(this);
    exp.exp2.visit(this);
  }
  void onSequence( SequenceExp exp ) {
    exp.exp1.visit(this);
    if(exp.exp1.isNullable())
      exp.exp2.visit(this);
  }
  void onElement( ElementExp exp ) {
    headElements.add(exp);
  }
  ....
}

class  Expression {
  ....
  abstract void getHeadElements( Set result );
}

class SequenceExp : Expression {
  ....
  void collectHeadElements( Set result ) {
    exp1.collectHeadElements(result);
    if(exp1.isNullable())
      exp2.collectHeadElements(result);
  }
}

class ElementExp {
  ....
  void collectHeadElements( Set result ) {
    result.add(this);
  }
}

By using these concepts, we are now ready to implement the whole validation algorithm.

The algorithm uses two internal state. exp is a variable that keeps the current derivative, and s is a stack that stores Expressions.

By using a DOM-like tree, the following pseudo-code describes this algorithm:

Expression validate( Expression grammar, DOMDocument doc ) {
    validate( grammar, doc.getRootElement() );
}

Expression validate( Expression exp, DOMElement e ) {

    ElementExp[] heads = exp.getHeadElements();
    remove ElementExps whose name class doesn't accept the tag name of e;
    
    // for today, we assume at most one ElementExp will be left.
    if(heads is empty)
        report that this element is not allowed and halt;
    
    Expression child = heads[0].contentModel;
    
    // process attributes
    for(each attribute a of this element)
        child = child.derivativeByAttribute(a);
    
    for(each DOMNode n in children of e ) {
        child = validate(child,n);
    }
    
    if(child is not nullable)
       report that some required elements are missing and halt;
    
    return exp.derivative(heads[0]);
}

Expression validate( Expression exp, DOMTextNode n ) {
    return exp.derivative(text of n);
}

Note that this algorithm processes documents in a forward-only fashion. Thus it should be easy to modify it to work with a pull parser or SAX.